功率密度谱(Power Spectral Density)笔记

这篇文章是学习使用匹配滤波方法(matched-filter method)从记录中提取信号时记录的系列笔记的第二篇，主要整理关于功率密度谱(power spectral density)及其计算方法的基本知识。

本文主要参考的资料为：

牛津大学Prof. David Murray的课程资料: https://www.robots.ox.ac.uk/~dwm/Courses/2TF_2011/2TF-N5.pdf
Barry Van Veen的系列课程: https://allsignalprocessing.com/course-introduction-information/
scipy.signal.periodogram: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.periodogram.html
scipy.signal.welch: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.welch.html
Welch, P. (1967). The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Transactions on audio and electroacoustics, 15(2), 70-73.

功率信号

一般来说，信号可以被分为两类，即能量信号(energy signal)和功率信号(power signal)。

对于能量信号，其总能量是有限的 \[ \begin{equation} E_{Tot} = \int_{-\infty}^{\infty} |f(t)|^2 dt, \quad 0<E_{Tot}<\infty \end{equation} \] 由于总能量是有限的，所以用其除以无限长的时间，得到信号的平均功率(average power)为零。

对于能量信号$f(t)$，

总有Fourier变换$F(f)$;
总有能量谱密度(energy spectral density, ESD) $ \mathcal{E}_{ff}(f)= \lvert F(f) \rvert ^2 $;
总有自相关$R_{ff}(\tau) = \int_{-\infty}^{\infty} f(t)f(t+\tau) dt$;
ESD和自相关是Fourier变换对 $\mathcal{E}_{ff}(f) = \int _{- \infty }^{ \infty } R _{ff}(\tau) e^{-i2\pi f \tau} d\tau$, $R _{ff}(\tau) = \int _{- \infty }^{ \infty } \mathcal{E} _{ff}(f) e^{i2\pi f \tau} df $;
总能量为 $E_{Tot} = R_{ff}(0) = \int_{-\infty}^{\infty} \mathcal{E}_{ff}(f) df$
ESD在经过线性系统后 $\mathcal{E} _{gg}(f)=\lvert H(f)\rvert ^2\mathcal{E} _{ff}(f)$

对于功率信号，其总能量是无穷大的，平均功率表示为 \[ \begin{equation} P_{Ave} = \lim \limits_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} |f(t)|^2 dt, \quad 0<P_{Ave}<\infty \end{equation} \] 对于功率信号$f(t)$，

也许有Fourier变换$F(f)$;
也许有功率谱密度(power spectral density, PSD) $ S_{ff}(f)= \lvert F(f) \rvert ^2 $;
总有自相关$R_{ff}(\tau) = \lim\limits_{T \to \infty} \frac{1}{2T}\int_{-T}^{T} f(t)f(t+\tau) dt$;
PSD和自相关是Fourier变换对 $S_{ff}(f) = \int _{- \infty }^{ \infty } R _{ff}(\tau) e^{-i2\pi f \tau} d\tau$, $R _{ff}(\tau) = \int _{- \infty }^{ \infty } S _{ff}(f) e^{i2\pi f \tau} df $;
平均功率为 $P_{Ave} = R_{ff}(0)$
PSD在经过线性系统后 $S _{gg}(f)=\lvert H(f)\rvert ^2 S _{ff}(f)$.

随机过程的功率谱密度(power spectral density)

功率谱密度代表了一个稳态随机过程在频率域的特征，表示在一个频率间隔内的成分对于总平均功率的贡献。从之前的结论中也能看出，PSD是信号自相关函数的Fourier变换。

PSD tells us how the contributions of power are distributed in frequency.

性质

以离散信号$ \left\lbrace x[n], -\infty <n<\infty \right\rbrace $为例

单位与量纲: $S(F)-\mathrm{power/Hz}$;
平均功率$R[0] = \int _{-f_s/2 }^{f_s/2} S(f)df = E[x^2[n]]$，其中$f_s$为采样频率;
$S(f) \ge 0$且为实数;
如果$x[n]$为实信号，那么$S(f)$为偶函数，即$S(f) = S(-f)$。

利用周期图(periodogram)计算PSD

估计PSD

对于离散信号$ \left\lbrace x[n], 0 \le n \le N-1 \right\rbrace $，根据之前的分析，我们知道其功率谱密度是自相关的Fourier变换，其自相关为 \[\begin{equation} R_{xx}[k] = E[x(n)x(n-k)] = \frac{1}{N} \sum_{n=0}^{N-1} x[n]x[n-k] \end{equation}\] 所以功率谱密度$\hat{S} _{xx}(f)$为 \[ \begin{equation} \begin{split} \hat{S} _{xx}[p] & = \mathscr{F}[R _{xx}[k]] = \sum _{k=0}^{N-1} \left\lbrace \frac{1}{N} \sum _{n=0}^{N-1} x[n]x[n-k] \right\rbrace e^{-i2\pi kp/N} \\
& = \frac{1}{N} \sum _{l=n-N-1}^{n} \sum _{n=0}^{N-1} x[n]x[l] e^{-i2\pi np/N} e^{i2\pi lp/N} \\
& = \frac{1}{N} \sum _{l=0}^{N-1} x[l] e^{i2\pi lp/N} \sum _{n=0}^{N-1} x[n] e^{-i2\pi np/N} \\
& = \frac{1}{N} X^{*}[p] X[p] \\
& = \frac{1}{N} \lvert X[p] \rvert ^2 \end{split} \end{equation} \] 因为这里采用的均是离散Fourier变换(DFT)，所以在计算之后还要对$\hat{S} _{xx}$进行归一化，从而使得功率谱密度下方的面积等于总的平均功率，即 \[\begin{equation} \int _{0}^{fs/2} \hat{S} _{xx}(f) df = R _{xx}(0) \end{equation}\] 这也就是令$\hat{S} _{xx}$具有$\mathrm{power/Hz}$的量纲。归一化之后的$\hat{S} _{xx}$可以表示为 \[\begin{equation} \hat{S} _{xx}(f_p) = \hat{S} _{xx}(\frac{p f_s}{N}) = \hat{S} _{xx}[p] \frac{2}{f_s} = \frac{2}{f_s N} \lvert X[p] \rvert ^2 \end{equation}\] 需要说明的是，由于信号往往为实信号，根据前面的 性质5 ,这里在对PSD积分时，我们只考虑了正频率的部分，即$0 \le f \le fs/2$，所以得到对应的归一化后的PSD为单边PSD(one-sided power spectral density)。

对于这一点，我们也可以从另一个角度进行分析。在使用离散Fourier变换(DFT)$H_n$来估计连续时间的Fourier变换$H(f_n)$时，我们有关系 \[\begin{equation} \begin{split} H(f_n) & = \int _{-\infty}^{\infty} h(t) e^{-i2\pi f _n t}dt \\
& \approx \sum _{k=0}^{N-1} h _k e^{-i2\pi f _n t _k} \Delta = \Delta \sum _{k=0}^{N-1} h _k e^{-i2\pi nk/N} \end{split} \end{equation}\] 即 \[\begin{equation} H(f_n) \approx \Delta H_n \end{equation}\] 其中$H_n$为N个点的DFT \[\begin{equation} H_n = \sum _{k=0}^{N-1} h _k e^{-i2\pi nk/N} \end{equation}\] $\Delta$为连续时间序列的采样间隔，$h_k=h(t_k)=h(k\Delta)$。

类比这一思路，我们可以分析如何使用离散点计算的PSD ($\hat{S} _{xx}[p]$)来估计连续的PSD($\hat{S} _{xx}(f_p)$) \[\begin{equation} \begin{split} \hat{S} _{xx}(f_p) & = \mathscr{F}[R _{xx}(\tau)] = \int _{-\infty}^{\infty} R _{xx}(\tau) e^{-i2\pi f_p \tau} d\tau \\
& = \int _{-\infty}^{\infty} \left\lbrace \lim\limits _{T \to \infty} \frac{1}{T} \int _{-T/2}^{T/2}x(t)x(t-\tau) dt \right\rbrace e^{-i2\pi f_p \tau} d\tau \\
& \approx \sum _{k=0}^{N-1} \left\lbrace \frac{1}{N \Delta} \sum _{n=0}^{N-1} x[n]x[n-k] \Delta \right\rbrace e^{-i2 \pi pk/N} \Delta \end{split} \end{equation}\] 根据公式(4)，我们可以得到 \[\begin{equation} \hat{S} _{xx}(f_p) = \hat{S} _{xx}[p] \Delta = \frac{1}{f_s} \lvert X[p] \rvert ^2 \end{equation}\] 这里我们没有限制$f_p$必须大于零，所以得到的PSD为双边PSD(two-sided power spectral density)。 \[\begin{equation} S _{xx}^{one}(f) = 2 S _{xx}^{two}(f) \end{equation}\]

一般步骤

在实际计算中，使用周期图(periodogram)方法来计算PSD时，往往会对信号加各种窗函数(直接计算相当于使用矩形窗)，从而使得结果更加平滑。

给信号加窗：$x_w[n] = x[n]w[n]$，$0 \le n \le N-1$;
进行DFT：$X_w[p] = \mathscr{F}[x_w[n]]$;
估计PSD：$\hat{S} _{xx}[p] = \frac{1}{NF} \lvert X_w[p] \rvert ^2$.

其中$w[n]$为窗函数，$F = \frac{1}{N} \sum _{n=0}^{N-1} (w[n])^2$，以及$X_w[p] = \mathscr{F}[x[n]w[n]]$

周期图法估计的PSD的性质

这一部分目前只列出结论，还没进行推导或验证。

均值 \[\begin{equation} E\left\lbrace \hat{S} _{xx}(f) \right\rbrace = \frac{1}{NF} \int _{-fs/2}^{fs/2} S _{xx}(f’)C _{ww}(f-f’) df’ \end{equation}\] 其中 \[\begin{equation} C _{ww}(f) = \lvert W(f) \rvert ^2 = \lvert \mathscr{F}[w(t)] \rvert ^2 \end{equation}\] 公式(13)右侧可以看作是真实的PSD$S _{xx}(f)$和$C _{ww}(f)$的卷积。当窗长变大时，$W(f)$的主瓣宽度会减小，$C _{ww}(f)$也更集中于$f=0$，所以 \[\begin{equation} E\left\lbrace \hat{S} _{xx}(f) \right\rbrace \rightarrow S _{xx}(f) \end{equation}\] 因此周期图方法对于PSD的估计是渐进无偏(asymptotically unbiased)估计。
方差 \[\begin{equation} var\left\lbrace \hat{S} _{xx}(f) \right\rbrace \rightarrow S^2 _{xx}(f) \end{equation}\] 周期图方法不是PSD的一致估计(not a consistent estimator)。

利用Welch方法计算PSD

Welch方法可以看作是对周期图方法的一种改进，同时使用加窗处理和平均处理，可以有效降低PSD估计的方差(Welch, 1967)。

计算步骤

对于一个离散时间序列$ \left\lbrace x[n],\quad n=0,1,…,N-1 \right\rbrace $，将其划分为K个子序列，每个序列长度为L，子序列之间可以有重叠，相邻两个子序列起始位置间隔为D，这样我们有关系$N=L+(K-1)D$，而对于第$k(k=1,2,…,K)$个子序列的第$l(l=0,1,…,L-1)$个元素$x^k[l]$，其在原序列中的位置为$x^k[l]=x[l+D(k-1)]$，具体关系如图所示

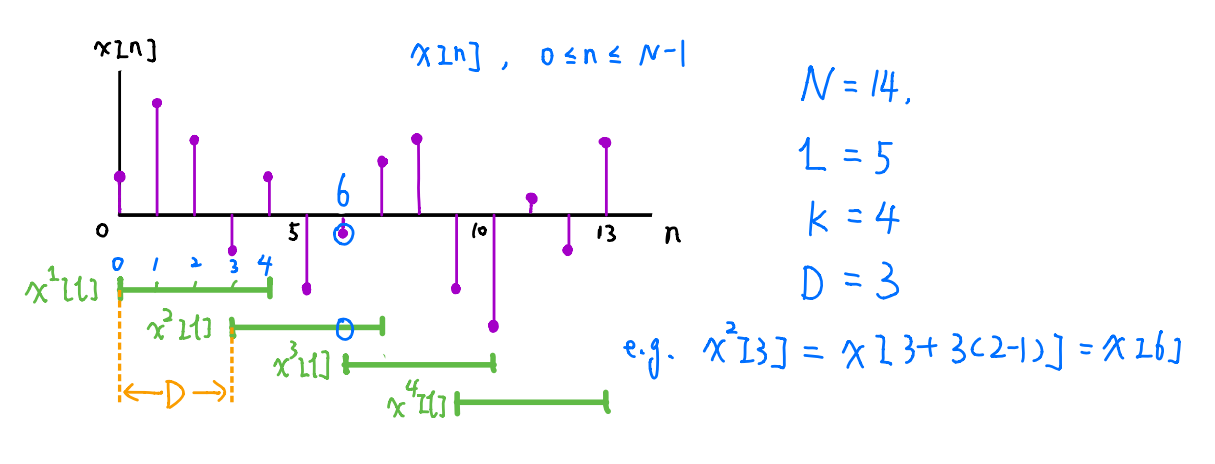
PSD-Welch

计算每个子序列在加窗后的Fourier变换 \[ \begin{equation} X^k_w[j] = \frac{1}{L} \sum _{l=0}^{L-1} x^k[l]w[l] e^{-i2\pi lj/L} \end{equation} \] 其中$\left\lbrace w[l],\quad l=0,1,…,L-1 \right\rbrace$为窗函数;
计算每个子序列的加窗后的周期图(modified periodogram) \[ \begin{equation} I^k[j] = \frac{L}{F} \lvert X^k_w[j] \rvert ^2 \end{equation} \] 其中$F$的定义与上一节类似 \[ \begin{equation} F = \frac{1}{L} \sum _{l=0}^{L-1} (w[l])^2 \end{equation} \]
对每个子序列的周期图进行平均，得到利用Welch方法的PSD估计 \[ \begin{equation} \hat{S} _{xx}[j] = \frac{1}{K} \sum _{k=1}^{K} I^k[j] \end{equation} \]

可以看出，当$K=1$，即$L=N$时，Welch方法就是加窗的周期图方法。

Welch方法估计的PSD的性质

这一方法得到的估计仍是渐进无偏估计;
对于Welch估计$\hat{S} _{xx}^{Wel}(f)$的方差，我们有 \[ \begin{equation} \frac{1}{K} var\left\lbrace \hat{S} _{xx}^{per}(f) \right\rbrace \le var\left\lbrace \hat{S} _{xx}^{Wel}(f) \right\rbrace \le var\left\lbrace \hat{S} _{xx}^{per}(f) \right\rbrace \end{equation} \] 其中$\hat{S} _{xx}^{per}(f)$为周期图方法对于PSD的估计。

在使用Welch方法进行估计时，如果子序列之间没有重叠，即$D=L$，则 \[ \begin{equation} var\left\lbrace \hat{S} _{xx}^{Wel}(f) \right\rbrace = \frac{1}{K} var\left\lbrace \hat{S} _{xx}^{per}(f) \right\rbrace \end{equation} \]

利用Python计算PSD的例子

在这一部分中，展示对于同一段信号，分别采用周期图(periodogram)方法和Welch方法计算得到的功率谱密度PSD。

输入信号$x(t)$为由一个正弦信号$s(t) = 0.4 \sin (2 \pi f_0 t), f_0=1.0Hz$ 和取样自$x \sim N(0,0.01)$的高斯白噪音(Gaussian white noise)$n(t)$组成，即$x(t)=s(t)+n(t)$，采样率为10Hz，时间序列长度为100s.

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

# Set parameters
fs = 10
Ttotal = 100
time = np.arange(fs*Ttotal) / fs
# Simulate noise n(t)
noise_power = 0.01 * fs / 2
x_nois = np.sqrt(noise_power) * np.random.randn(len(time))
# Simulate signal s(t)
f0 = 1.0
sigl_amp = 0.4
x_sigl = sigl_amp * np.sin(2*np.pi*f0*time)

# x(t) = s(t)+n(t)
x = x_nois + x_sigl
# plot time series
plt.figure(figsize=(12,6))
plt.plot(time, x)
plt.xlabel('Time [s]',fontsize=14)
plt.xticks(fontsize=14)
plt.ylabel('Amp',fontsize=14)
plt.yticks(fontsize=14)
plt.show()

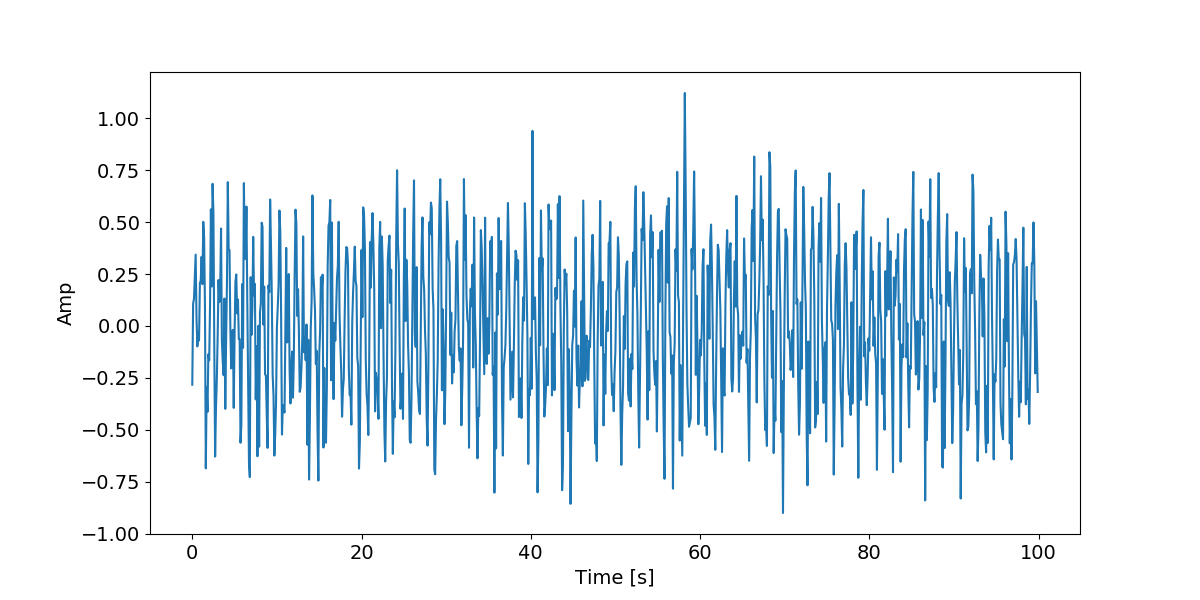
PSD-time-series

使用周期图法估计PSD

# Periodogram
# no window
freq, Sxx_per = signal.periodogram(x, fs)
# with a Hanning window
freq, Sxx_per_w = signal.periodogram(x, fs, window='hanning')
plt.figure(figsize=(12,6))
plt.semilogy(freq, Sxx_per, label="no window", color = 'blue')
plt.semilogy(freq, Sxx_per_w, label='Hanning window', color = 'red')
plt.xlabel('Frequency [Hz]',fontsize=14)
plt.xticks(fontsize=14)
plt.ylabel('PSD [1/Hz]',fontsize=14)
plt.yticks(fontsize=14)
plt.ylim([1.0E-6,1.0E2])
plt.legend(fontsize=14)
plt.show()

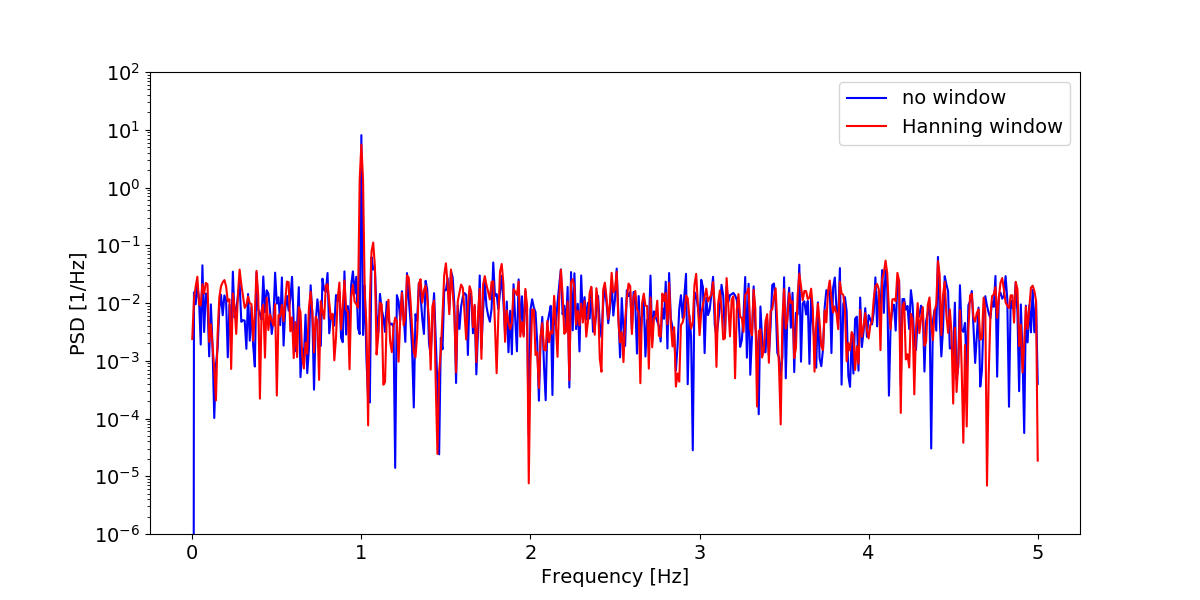
PSD-per

使用Welch法估计PSD

# Welch Method
# with a Hanning window
freq_wel_1, Sxx_wel_1 = signal.welch(x, fs, nperseg=500)
freq_wel_2, Sxx_wel_2 = signal.welch(x, fs, nperseg=250)
plt.figure(figsize=(12,6))
plt.semilogy(freq, Sxx_per_w, label='periodogram', color = 'red',linewidth='1')
plt.semilogy(freq_wel_1, Sxx_wel_1, label="Welch(L=500)", color = 'lawngreen', linewidth='3')
plt.semilogy(freq_wel_2, Sxx_wel_2, label="Welch(L=250)", color = 'darkgreen', linewidth='2')
plt.xlabel('Frequency [Hz]',fontsize=14)
plt.xticks(fontsize=14)
plt.ylabel('PSD [1/Hz]',fontsize=14)
plt.yticks(fontsize=14)
plt.ylim([1.0E-6,1.0E2])
plt.legend(fontsize=14)
plt.show()

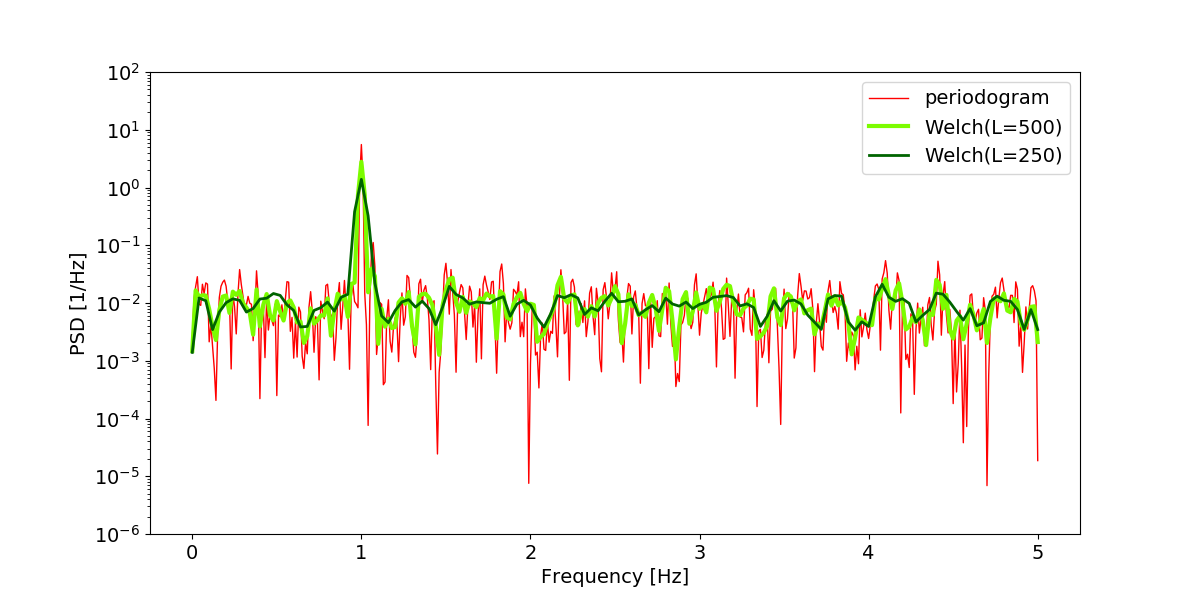
PSD-wel

从结果我们可以看出Welch方法对于PSD的平滑作用，以及较短的子序列虽然会增加子序列数量(在重叠相同时)，从而提高平均效果，但是也会降低频率分辨率。

一点讨论

最后需要说明的一点是，从代码中可以看出，对于噪音$n(t)$，虽然设置其Gauss分布为$N(0,0.01)$，但是在程序中其振幅为

noise_power = 0.01 * fs / 2
x_nois = np.sqrt(noise_power) * np.random.randn(len(time))

这是因为PSD是自相关的Fourier变换，即 $S_{xx}(f) = \mathscr{F}[R_{xx}(\tau)]$，而对于高斯白噪音，$R_{nn}(\tau)=\sigma^2 \delta(\tau)$，其中$\sigma^2$为高斯分布的方差，在使用离散数据点进行计算时，$\delta$-函数只能用有限大小的振幅来近似，对于时间间隔为$\Delta$的采样来说，$R_{nn} (0)$的采样$R_{nn}[0]=\sigma^2 f_s$，从而使得$\int R_{nn}(\tau) d\tau = \sum_k R_{nn}[k] \Delta = \sigma^2$，这样在对$\hat{S}_{nn}[p]$按照之前的方式归一化之后，得到的结果为$E \left\lbrace \hat{S} _{nn}(f_p) \right\rbrace = \sigma^2$，从而与连续函数的结果一致。

更进一步地，我们可以类比分析$x(t)$中的信号部分$s(t)$，对于给定的$s(t)=A \sin (2\pi f_0 t)$，易知其自相关为$R _{ss}(\tau) = A^2/2 \cos(2\pi f_0 \tau)$，这样离散的PSD估计为 \[ \begin{equation} \begin{split} \hat{S} _{ss}[p] & = \sum _{k=0}^{N-1} \frac{A^2}{2} \cos (2\pi f_0 k\Delta) e^{-i2\pi k p/N} \\
& = \frac{A^2}{4} \sum _{k=0}^{N-1} \left\lbrace e^{i2\pi n_0k/N} + e^{-i2\pi n_0k/N} \right\rbrace e^{-i2\pi kp/N} \\
& = \frac{A^2}{4} \sum _{k=0}^{N-1} \left\lbrace e^{-i2\pi (n+n_0) k/N} + e^{-i2\pi (n-n_0) k/N} \right\rbrace \\
& = \frac{A^2}{4} \left [ \delta(n-n_0) + \delta(n+n_0) \right ] \frac{1}{\Delta} \end{split} \end{equation} \] 类似前面的方式考虑离散情况下的$\delta$-函数，以及PSD的偶函数性质，我们有单边PSD的估计 \[ \begin{equation} \hat{S} _{ss}[p] = \frac{A^2}{2} \frac{1}{df} \frac{1}{\Delta} = \frac{A^2}{2} T f_s \end{equation} \] 其中$T=N \Delta$为采样的总长度。

这样按照同样的方法归一化后 \[ \begin{equation} E \left\lbrace \hat{S} _{ss}(f_p) \right\rbrace = \frac{A^2}{2} T \end{equation} \] 这些结果都能在前面的图中得到验证。

这一部分内容主要是帮助自己理解Python官方对于signal.periodogram和signal.welch函数的示例脚本在模拟噪音时是如何设其振幅的，这部分内容在数学上并不严格，但是能较好解释一些问题，所以也一起写了下来。