SPECFEM3D_GLOBE中网格(mesh)的可视化

这篇文章是我在学习使用理论地震图计算软件SPECFEM3D_GLOBE时，针对其划分的网格(mesh)的可视化问题所整理的一些笔记。

注意：如果第一次打开本网页时公式显示出现问题，只需要刷新即可。

网格的生成

Specfem3D_Globe是一个基于谱元法(Spectral element method)来计算理论地震图的程序(reference)，其主要编程语言为Fortran和C。与有限元方法类似，在最终求解之前，都要先进行离散化，单元分析和总体分析。在编程实践中，Specfem3D_Globe通过编译Fortran代码生成的可执行文件 xmeshfem3D 来实现网格划分、单元分析和总体分析。在这一部分中，简单介绍一下Specfem3D划分网格的方法，包括理论基础以及相关代码。详细的介绍可以参考Komatitsch & Tromp (2002)。

Spefem3D_Globe采用的是六面体单元(hexahedral finite element)，具体来说是相容六面体单元(conforming element)，表现为每个六面体单元可以和邻近的单元完全贴合。

映射(Mapping)

对于一个单元 $\Omega_e$ 中笛卡尔坐标下的点$\mathbf{x}=(x,y,z)$，我们有其与参考单元的映射： \[ \begin{equation} \mathbf{x}(\boldsymbol{\xi})=\sum_{a=1}^{n_a} N_a(\boldsymbol{\xi}) \mathbf{x_a} \end{equation} \] 其中$\boldsymbol{\xi}=(\xi,\eta,\zeta), -1\leq\xi,\eta,\zeta \leq 1$。$\mathbf{x_a}$为控制点(control points, or anchors)。

在Spefem3D_Globe中，对六面体单元采用了27个控制点(Komatitsch & Tromp, 2002, Figure 1)。相应地，形函数(shape function)$N_a$为3个二阶Lagrange多项式的乘积，例如 \[ \begin{equation} N_1(\boldsymbol{\xi}) = l_1(\xi)l_1(\eta)l_1(\zeta)=\frac{1}{2}\xi(\xi-1)\frac{1}{2}\eta(\eta-1)\frac{1}{2}\zeta(\zeta-1) \end{equation} \] 对于如CMB和ICB这样固-液间断面上的2D网格，采用类似的分析可以得到相应的2D映射关系。

Cubed sphere

Specfem3D_Globe在对全球进行网格划分，以及之后的并行求解中，首先将地球表面划分为6个部分(8个“铰合点”)，也就是利用“quasi-uniform gnomonic projection”的投影方法，将一个六面体的六个面投影到一个球面上，这样六面体每个面上的等距离网格就转换成相应球面上等角度的网格(Komatitsch & Tromp, 2002, Figure 2)。对于地球模型来说，我们在地表和ICB分别进行一次这样的投影，可以得到6个块体(chunks)，并在径向通过插值就可以得到初步的全球网格划分。但是这样得到的网格存在相应的问题，随着深度增加，网格尺寸越来越小，而根据速度模型，地震波波速随深度越来越大(一般情况下)，这样就导致谱元法求解地震波场的要求之一的“一个波长中包含数量近似的网格节点”无法满足。所以，在上述网格划分的基础上，还要引入网格放大(mesh doubling)，具体的放大方法见(Komatitsch & Tromp, 2002, Figure 4)。在实际计算中，程序在Moho面下方，670km间断面下方和ICB上方分别进行了3次网格放大，也就是说对于一个在表面有240*240单元的块体，其在ICB处只有30*30个单元。

单元分析

对于谱元法求解，与有限元方法类似，首先需要写出偏微分方程的弱形式(weak form)。简单起见，这里忽略重力和自转对地震波传播的影响，同时只以地壳-地慢为例，得到运动方程的弱形式： \[ \begin{equation} \int_{M} \rho \mathbf{w}\cdot\partial_{t}^2 \mathbf{s} dV = \int_{M} \nabla\mathbf{w}:\mathbf{T} dV + \mathbf{M}:\nabla\mathbf{w}(\mathbf{r_s})S(t) - \int_{CMB} \mathbf{w} \cdot \mathbf{T} \cdot \hat{n} dS \end{equation} \] 符号的具体含义参考(Komatitsch & Tromp, 2002, Section 3.1)。

下一步就是如何在单元中表示如位移$\mathbf{s}$这样的未知量。与传统有限元法采用等参单元，即坐标和未知量近似解采用相同的低阶形函数不同的是，谱元法采用低阶多项式(形函数)描述单元形状，但采用高阶多项式(形函数)来表示未知量。具体表现为对于函数$f(\mathbf{x}(\xi,\eta,\zeta))$，其近似表示为 \[ \begin{equation} f(\mathbf{x}(\xi,\eta,\zeta)) \approx \sum_{\alpha,\beta,\gamma=0}^{n_{\alpha},n_{\beta},n_{\gamma}} f^{\alpha\beta\gamma} l_{\alpha}(\xi) l_{\beta}(\eta) l_{\gamma}(\zeta) \end{equation} \] 其中形函数是三组4阶Lagrange多项式(每一组有5个控制点)$l_{\alpha}(\xi)$，$l_{\beta}(\eta)$，$l_{\gamma}(\zeta)$的乘积，多项式$l_{\alpha}$的形式见(Komatitsch & Tromp, 2002, Eq.25)。

这里需要注意的是，对于任一Lagrange所需要的5个控制点并不是任意选取的，而是选择5个Gauss-Lobatto-Legendre点，这种选取方法会大大简化之后的积分计算以及时间域的求解。应用Gauss–Lobatto–Legendre积分规则，单元上的积分可以写为(Komatitsch & Tromp, 2002, Eq.29) \[ \begin{equation} \int_{\Omega_e}f(\mathbf{x}) dV \approx \sum_{\alpha,\beta,\gamma=0}^{n_{\alpha},n_{\beta},n_{\gamma}} \omega_{\alpha}\omega_{\beta}\omega_{\gamma} f^{\alpha\beta\gamma} J^{\alpha\beta\gamma} \end{equation} \] 其中$J^{\alpha\beta\gamma}=\vert\frac{\partial(x,y,z)}{\partial(\xi,\eta,\zeta)}\vert$，$\omega_{\alpha}，\omega_{\beta}，\omega_{\gamma}$为Gauss–Lobatto–Legendre求积中的权重因子。

总体分析和求解

对于弱形式中的每一项，我们都可以通过上两式的形式转化为相应的求和形式，从而得到单元中的控制方程，再通过总体分析，组集(assemble)(组集由求解程序xspecfem3D完成)得到全局的时间域常微分方程(Komatitsch & Tromp, 2002, Eq.46) \[ \begin{equation} \pmb{M\ddot{U}}+\pmb{KU}+\pmb{BU}=\pmb{F} \end{equation} \] 之后通过经典的显式二阶有限差分方法即可求解。

到这里，我们大概可以看出Specfem3D_Globe的求解思路了，当然这里省略了相当多的推导细节和计算技巧，只是展示最基本的求解流程和思路。对于网格划分程序xmeshfem3D来说，其主要完成的是到单元分析为止的步骤。在可视化中，我们可以通过单元的节点来观察网格形状，以及每个单元中一些物理量或各种特征。

相应代码实现

在这一步分中，我会简单介绍程序xmeshfem3D中一些自己认为重要的代码(换句话讲是我能看懂的部分)，从而展示前面的一些理论推导在具体计算中是如何实现的。

主程序xmeshfem3D 由6个子程序(subroutine)构成，各自作用如下 subroutines_1st

为了加快网格划分速度、减少内存，xmeshfem3D 采用了并行编程计算(例如MPI库)的方法，具体表现为，对于在 Cubed sphere 中组成全球介质的6个块体(chunk)中的任一个，再将其划分为NPROC_XI*NPROC_ETA 个分割(slice)，每个分割(slice)上的网格划分在一个处理器(processor)上完成。对于每个单独的分割(slice)或者说在每个单独的处理器(processor)上，网格的划分是从三个层面上完成的。

首先，介质在径向上被划分为地壳和地慢、外核和内核3个区域(region)，对应的索引分别是IREGION_CRUST_MANTLE=1, IREGION_OUTER_CORE=2 和IREGION_INNER_CORE=3，在每个区域(region)中，网格的划分是在层(layer)的层面上进行的，层(layer)的划分则是根据地球内部的间断面，如Moho面、410km间断面、660km间断面等，以单一地壳的1D地球模型为例，地球由地表到地核被划分为13层，即NUMBER_OF_MESH_LAYERS=13，每个区域(region)中对应的层(layer)在子程序initialize_layers中由ifirst_region和ilast_region定义。最后，在任一层(layer)中（如第ilayer层)，介质被最终划分为一个个的单元(elements)，垂向的单元数目由设定的每层单元数ner(ilayer)来确定，水平向由NEX_PER_PROC_XI=NEX_XI/NPROC_XI、NEX_PER_PROC_ETA=NEX_ETA/NPROC_ETA以及单元放大倍数ratio_sampling_array(ilayer)所确定。

具体到相应的子程序，在子程序create_meshes()中，对3个区域(region)进行循环，在每个循环中，对于每一个区域(region)，首先得到这个区域中的单元和GLL节点数目nspec,nglob,npointot，之后通过调用子程序create_regions_mesh(...)来对该区域进行网格划分，计算单元中GLL节点位置和介质参数，并写入文件。在子程序create_regions_mesh(...)中，首先调用crm_setup_layers(...)来计算自然坐标系中GLL节点的位置，相应的权重，和形函数及其导数在这些节点的取值，之后调用create_regions_elements(...)，在这一子程序中，通过对区域中的层(layer)进行循环，在每个循环中调用create_regular_elements(...)来生成这一层中的网格单元，在生成网格单元时，通过compute_coord_main_mesh(...)来计算各单元27个控制点在地球中的相对位置xelem(27), yelem(27), zelem(27)，之后调用compute_element_properties(...)得到单元内125个GLL节点的位置和介质参数rhostore, kappavstore等。在create_regions_elements(...)计算完成后，再调用create_mass_matrices(...)计算质量矩阵(mass matrix)(Komatitsch & Tromp, 2002, Eq.33 & 46)在GLL节点处的值。最后调用子程序save_arrays_solver(...)将前面计算得到的结果写入相应的二进制文件中。程序流程示意图如下：

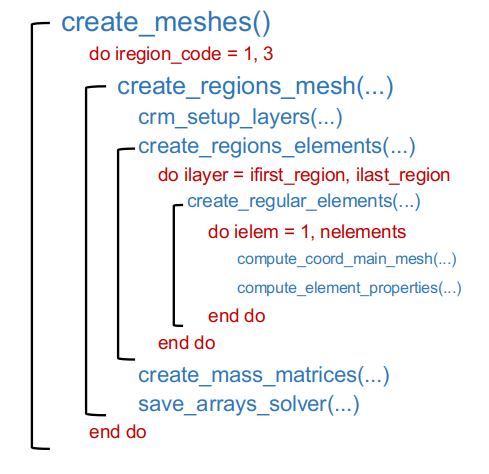
网格的可视化

可视化步骤

这里虽然我们采用程序Paraview来进行网格可视化，但是我们并没有采用.vtk格式的文件，而是采用AVS对应的.inp文件，Paraview同样可以读取这一格式的文件。为了得到这一文件，首先，我们需要将参数文件/DATA/Par_file中的SAVE_MESH_FILES选项设为true，这样运行xmeshfem3D后会生成相应的数据文件。我们在程序根目录中编译后处理程序 xcombine_AVS_DX，并在DATABASES_MPI的上级目录中运行，这一程序的作用是根据使用者的输入参数，将xmeshfem3D生成的各分割(slice)的数据文件组合成AVS/UCD格式。下面以程序中的例子~/EXAMPLES/regional_Greece_small/为例，来展示如何得到UCD格式的数据文件。

$ cd ~/EXAMPLES/regional_Greece_small/
$ ./run_this_example.sh
$ cd ../../
$ make xcombine_AVS_DX
$ cp xcombine_AVS_DX ~/EXAMPLES/regional_Greece_small/
$ cd ~/EXAMPLES/regional_Greece_small/
$ ./xcombine_AVS_DX

程序成功运行的话，会有如下显示

 Recombining all AVS or DX files for slices


 reading parameter file

 1 = create files in OpenDX format
 2 = create files in AVS UCD format
 any other value = exit

 enter value:

这里输入2选择生成AVS-UCD格式文件，点击回车之后，显示

 1 = edges of all the slices only
 2 = edges of the chunks only
 3 = surface of the model only
 any other value = exit

 enter value:

在这一步选择可视化单元的位置，注意这里只能展示每个块体(chunk)或分割(slice)外部的网格形状(1: 分割外侧; 2: 块体外侧; 3: 地表)。这里选择2，回车之后，显示

= color by doubling flag
= by slice number
= by CFL stability value of the time scheme
= by gridpoints per wavelength
= dvp/vp
= dvs/vs
= elevation of Earth model
= by region number
= focus on one doubling flag only
 any other value=exit

 enter value:

这里选择每个网格单元根据哪个变量来涂色，例如2表示根据不同分割(slice)的编号来涂色(Komatitsch & Tromp, 2002, Figure 9)，4表示根据单元中每个波长含有的格点数来涂色(Komatitsch & Tromp, 2002, Figure 8-a)。这里选择2,继续点击回车

1 = material property by doubling flag
2 = by slice number
3 = by region number
4 = by chunk number
any other value=exit

enter value:

除了单元颜色之外，还可以选择材料的性质，这里选择3，即不同的区域(region)在可视化中也可以被显示出来，再次点击回车

 enter first proc (proc numbers start at 0) =

输入起始处理器编号，如0

 enter last proc (enter -1 for all procs) =

这里输入-1表示所有处理器的结果都会被展示。

程序运行完成后，会在~/EXAMPLES/regional_Greece_small/OUTPUT_FILES中生成3个.inp文件: AVS_fullmesh.inp, AVS_epicenter.inp和AVS_source_reveivers.inp。之后运行Paraview，找到并打开刚刚生成的AVS_fullmesh.inp，“Properties”选项中的“Representation”选择Surface，“Coloring”选择Zcoord，得到结果

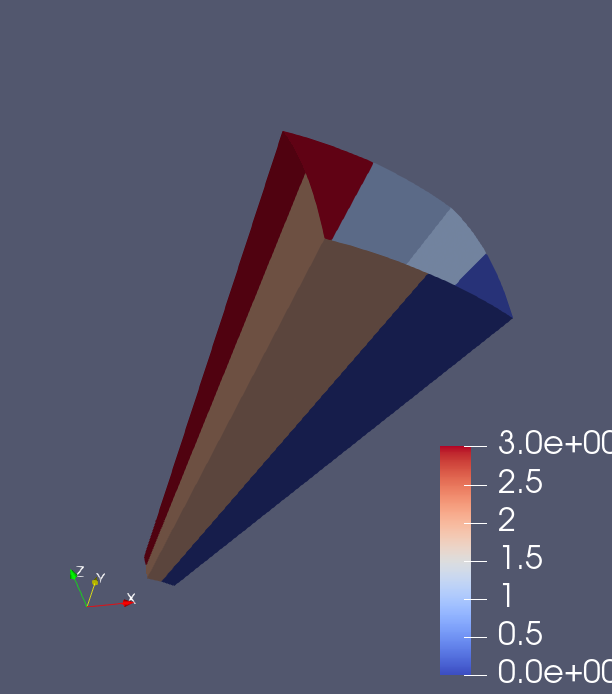
可以看到4个处理器对应的快体边界(edges of the chunk)被用4种颜色表示出来(edges只处理垂向边界，不考虑水平向边界，也就是地表)。之后我们可以再次运行xcombine_AVS_DX，只是在第二步的时候选择“3 = surface of the model only”，其余选项不变，生成另一个网格文件AVS_fullmesh.inp(为了区分两次计算的结果，可以先对上一次生成的文件进行重命名)，之后将新生成的文件也导入到Paraview中，与之前的结果一起展示，如图

之后将“Representation”设为Surface With Edges，同时绘制单元性质和网格节点，结果如下

对于Paraview中更多选项的设置，可以参考官方手册The ParaView Tutorial。

AVS-UCD文件格式

这一部分主要介绍上一节中程序xcombine_AVS_DX生成的AVS-UCD文件的格式，以便大家对单元网格有个更清晰的了解。这部分内容主要参考UCD Files和程序源代码文件~/src/auxiliaries/combine_AVS_DX.f90。

UCD 文件，全称为Unstructured Cell Data File，一般采用ASCII格式来存储网格单元结构，文件中可以包含网格单元的颜色信息，常见的后缀为.inp。一个ASCII格式的UCD文件主要由几个部分组成(需要注意的是，ASCII格式的UCD文件中不能包含有空行):

第一部分: 只有一行，共有5个值，分别表示节点(node)的个数 Nnode，单元(cell)的个数 Ncell，每个节点处的数据个数 Dnode，每个单元中的数据个数 Dcell，和模型数(一般均设为0);
第二部分: 所有网格节点的坐标(node coordinates)，共有 Nnode 行，每一行包含4个值，分别是节点的序号(node id)和节点的空间坐标(X,Y,Z);
第三部分: 所有单元的信息，共有 Ncell 行，每一行包含单元的序号(cell id)，单元的材料性质(material property)，单元类型(cell type)，最后是组成这一单元的节点的序号(ids of nodes that are associated with the cell);
第四部分: (如果有的话)只有一行，描述节点(node)上的数据，首先是节点处 Dnode 个数据被划分成的组数 Cnode，其次是每组数据分别包含几个值;
第五部分: (如果有的话)共有 Cnode 行，描述节点上每组数据的标签(label)和单位(unit)，中间用逗号隔开;
第六部分: (如果有的话)所有节点的数据，每行分别是节点序号(node ID)和该节点处的 Dnode 个具体数据;
第七部分-第九部分: 与第四部分-第六部分类似，只不过描述的是网格单元(cell)上的数据信息。

需要说明的是，在第三部分中，单元类型(cell type)由相应的字符串决定，常见的有 line, tri, quad, hex 等，分别表示线段，三角形，四边形和六面体。

下面以上一节中xcombine_AVS_DX生成的一个AVS-UCD文件AVS_fullmesh.inp为例，来展示相应的文件结构:

7112          6560  0 1 0
   1  0.8331280  0.2188696  0.4893440
   2  0.8290901  0.2232764  0.4883064
   3  0.8364307  0.2252533  0.4926298
   ...
   ...
7112  0.0960900  0.0809655  0.1445652
   1   1 quad      1      2      3      4
   2   1 quad      5      2      1      6
   3   1 quad      6      1      4      7
   ...
   ...
6560   3 quad   7091   7111   7112   7092
1 1
Zcoord, meters
      1     0.00000000
      2     0.00000000
      3     0.00000000
   ...
   ...
   6559     3.00000000
   6560     3.00000000

从第一行中我们可以看出，这一区域共有7112个节点以及6560个单元，在节点处没有数据存储，而每个单元对应1个数据。后面7112行是所有节点的序号和坐标。再之后6560行是单元的信息，需要注意的是每行第二个数据是单元的材料性质，在之前运行 xcombine_AVS_DX 时，我们选择材料性质根据区域编号来设定(by region number)，所以这一部分的第二列在1,2,3之中取值，分别代表地壳-地幔，外核和内核。由于第一行已经说明在节点处没有数据，所以之后一行表示每个单元数据的格式，即只有1组，1个数据，再下一行表示这个数据的标签和单位(从combine_AVS_DX.f90中其实可以看出，对于所有的单元数据类型，这里的标签和单位均为 Zcoord, meters)。最后6560行就是所有单元对应的数据，其对应的变量就是在运行 xcombine_AVS_DX 时我们选择的单元颜色对应的变量，由于我们之前选择的是不同分割的编号(by slice number)，所以文件中这一数据就从0-3中取值。

需要说明的一点是，在用Paraview对.inp文件中的单元进行可视化时，可以选择根据 Zcoord 还是根据 Material Id 来进行涂色(Zcoord 就是从.inp文件中读取的单元数据标签)，而由于 Material Id 只能是整型数据，所以只能选择如分割编号，块体编号等整型变量，而 Zcoord 没有这个限制，所以可以用来展示如波速变化(dvp/vp, dvs/vs)，CFL稳定系数等。

一些说明

在介绍谱元法计算理论地震图的理论时，只考虑了弹性球形介质的响应，忽略了重力、自转、椭球等的影响;
在介绍程序实现时，只分析了一些最为基本的子程序，例如只分析了一般块体中常规单元的生成方式，而没有考虑一般块体中的放大单元(doubling elements)和中心块体(central cube)中单元的生成过程;
这篇文章只着眼于谱元法计算中的网格单元生成过程，以及生成的网格单元的可视化，并没有涉及相应的方程求解。